分治法

使用分治法解决问题的基本步骤是：

• 分解： 将难以直接求解的复杂问题，分解成若干个规模较小、互相独立，且与原问题性质相同的子问题

• 求解： 将子问题分解至可直接求解

• 合并： 将子问题的解以某种方式合并成原问题的解

归并排序

归并排序的核心是：将两个连续的、各自有序的子序列合并成一个有序的子序列。

归并(array, start, mid, end) {
  // array[start...mid] 有序
  // array[mid+1...end] 有序
  // 最终使 array[start...end] 有序
  i = start;
  j = mid + 1;
  cursor = 0;
  temp_array = 长度是两个子序列长度之和的辅助数组;

  while (i <= mid && j <= end) {
    if array[i] <= array[j]
      temp_array[cursor++] = array[i++];
    else
      temp_array[cursor++] = array[j++];
  }

  如果第一个子序列没处理到头，则将第一个子序列中剩余的元素复制到 temp_array 的尾部;
  如果第二个子序列没处理到头，则将第二个子序列中剩余的元素复制到 temp_array 的尾部;

  将 temp_array 复制到 array[start...end];
}

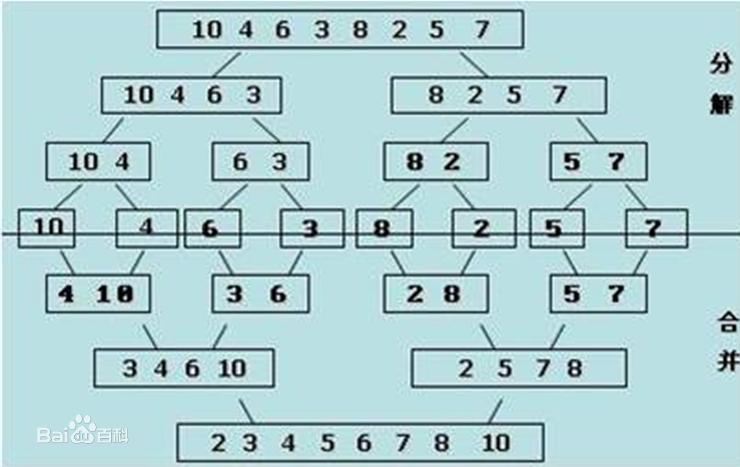
上面的算法是将子问题的解合并成原问题的解的方式，下面是一个分解-归并的整体过程的示例：

下面的伪代码是归并排序的递归实现：

归并排序(array, start, end) {
  if (end <= start)
    长度为 1 的子序列直接有序，直接返回;

  // 将子序列一分为 2，然后分别使用归并排序进行排序
  mid = (start + end) / 2;
  归并排序(array, start, mid);
  归并排序(array, mid+1, end);

  // 然后归并两个有序序列
  归并(start, mid, end);
}

时间复杂度

归并过程的时间复杂度是：n。

根据递归程序的时间复杂度计算公式，可得：

T(n) = 2 * T(n/2) + n ===>
T(n) = 2 * (2 * T(n/4) + n/2) + n ===>
T(n) = 4 * T(n/4) + 2 * n ===>
T(n) = 4 * (2 * T(n/8) + n/4) + 2 * n ===>
T(n) = 8 * T(n/8) + 3 * n ===>
...
T(n) = (2^m) * T(n/(2^m)) + m * n

且T(1) = 1

也就是当 n / (2^m) -> 1，即 m -> log2n 时，
T(n) = n + n * log2n
所以归并排序的时间复杂度是 O(nlogn)

空间复杂度

在归并时，用到了辅助数组，所以归并排序不是原地排序，其空间复杂度是 O(n)

Python 实现

tim-chow的 Gitub