给定一个二叉树,找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
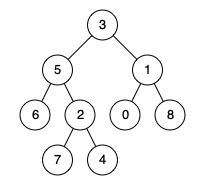
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
关于回溯算法,请参考:http://timd.cn/data-structure/backtrace/。
使用回溯算法搜索解空间,假设第一个找到的节点是 p,那么将 result 设置为 p,然后在以 p 为根的子树上搜索 q,如果找到了,那么 result 即为要求的结果;否则会回溯到 p 的父节点 pp,并将 result 设置为 pp,然后在以 pp 为根的子树上搜索 q,如果找到了,那么 result 即为要求的结果;否则回溯到 pp 的父节点 ppp,并将 result 设置为 ppp,...,直到找到 q 或解空间中没有活结点为止。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
if root is None or p is root or q is root:
return root
if p is q:
return p
stack = [root]
status = {}
result = None
while stack:
top = stack[-1]
if top is p or top is q:
if result is None:
result = top
elif top is not result:
return result
if top.val not in status:
status[top.val] = 0
if status[top.val] > 1:
status.pop(top.val)
stack.pop(-1)
if top is result:
if len(stack):
result = stack[-1]
else:
result = None
continue
if status[top.val] == 0:
next_node = top.left
else:
next_node = top.right
status[top.val] = status[top.val] + 1
if next_node is not None:
stack.append(next_node)
raise RuntimeError("unreachable")