KMP 算法

KMP 算法是具有跳跃性的字符串匹配算法。具体请参考百度百科。

在本文中，模式串是 Pattern，其长度为 m；待查找字符串是 MainString，其长度是 n。

next 数组

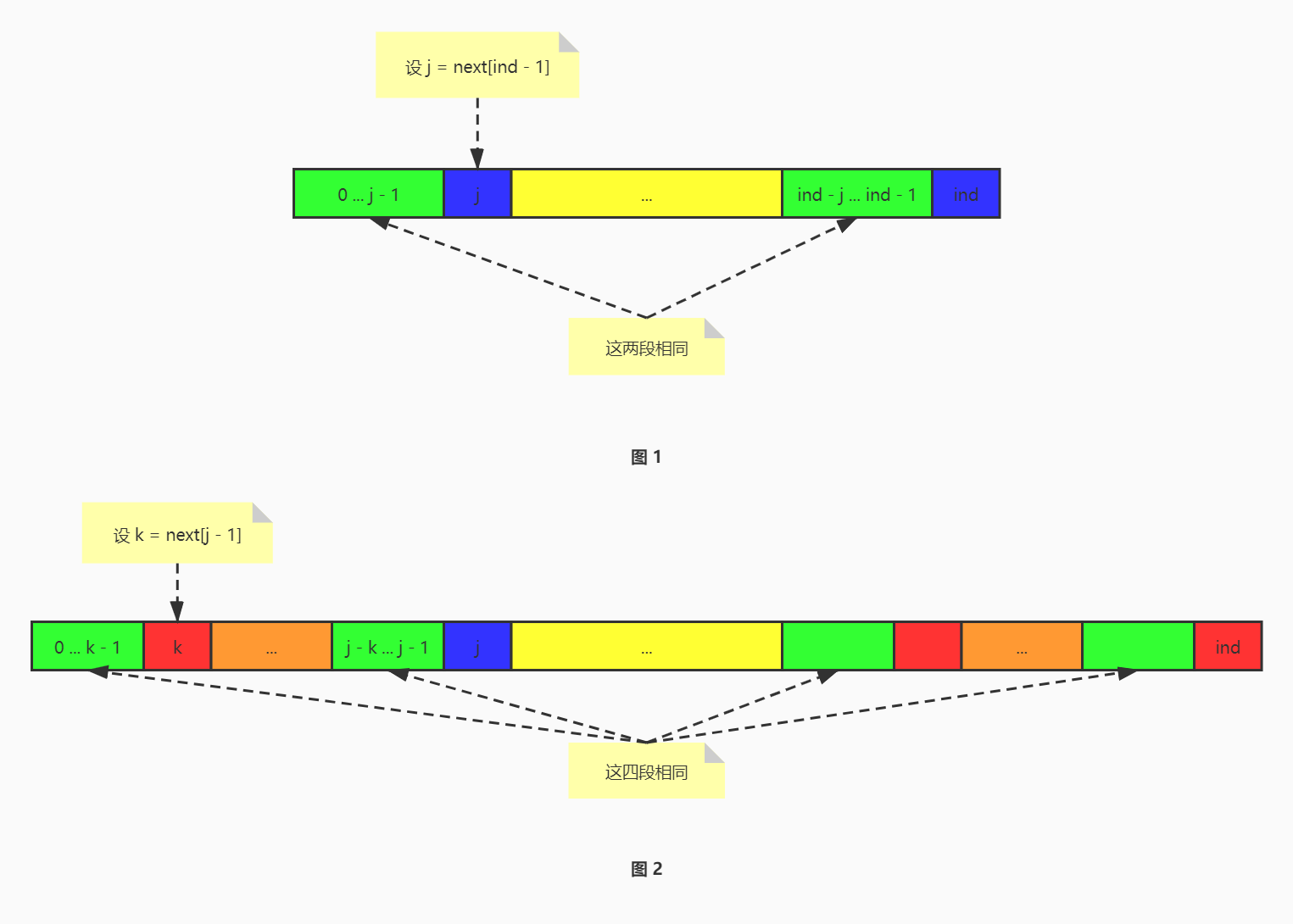
next[ind] 表示子串 Pattern[0 ... ind] 的最长公共前后缀的长度，其中 next[0] = 0。

在计算next数组时，可以根据前一个字符的 next 值，计算后一个字符的 next 值。

• 当 Pattern[ind] 等于 Pattern[j] 时，next[ind] = j + 1

• 否则：
  令 k = next[j - 1]

  1. 当 Pattern[ind] 等于 Pattern[k] 时，next[ind] = k + 1
  2. 当 k 等于 0 时，next[ind] = 0
  3. 否则，令 k = next[k - 1]，然后回到步骤 1

求 next 数组的伪代码如下：

数组 get_next(pattern) {
  next_array = 长为 m 的整型数组，初始时，所有元素都为0;
  for(ind = 1; ind < m; ind++) {
    j = ind;
    while (j > 0) {
      j = next_array[j - 1];
      if (pattern[ind] == pattern[j]) {
        next_array[ind] = j + 1;
        break;
      }
  }

  return next_array;
}

模式匹配

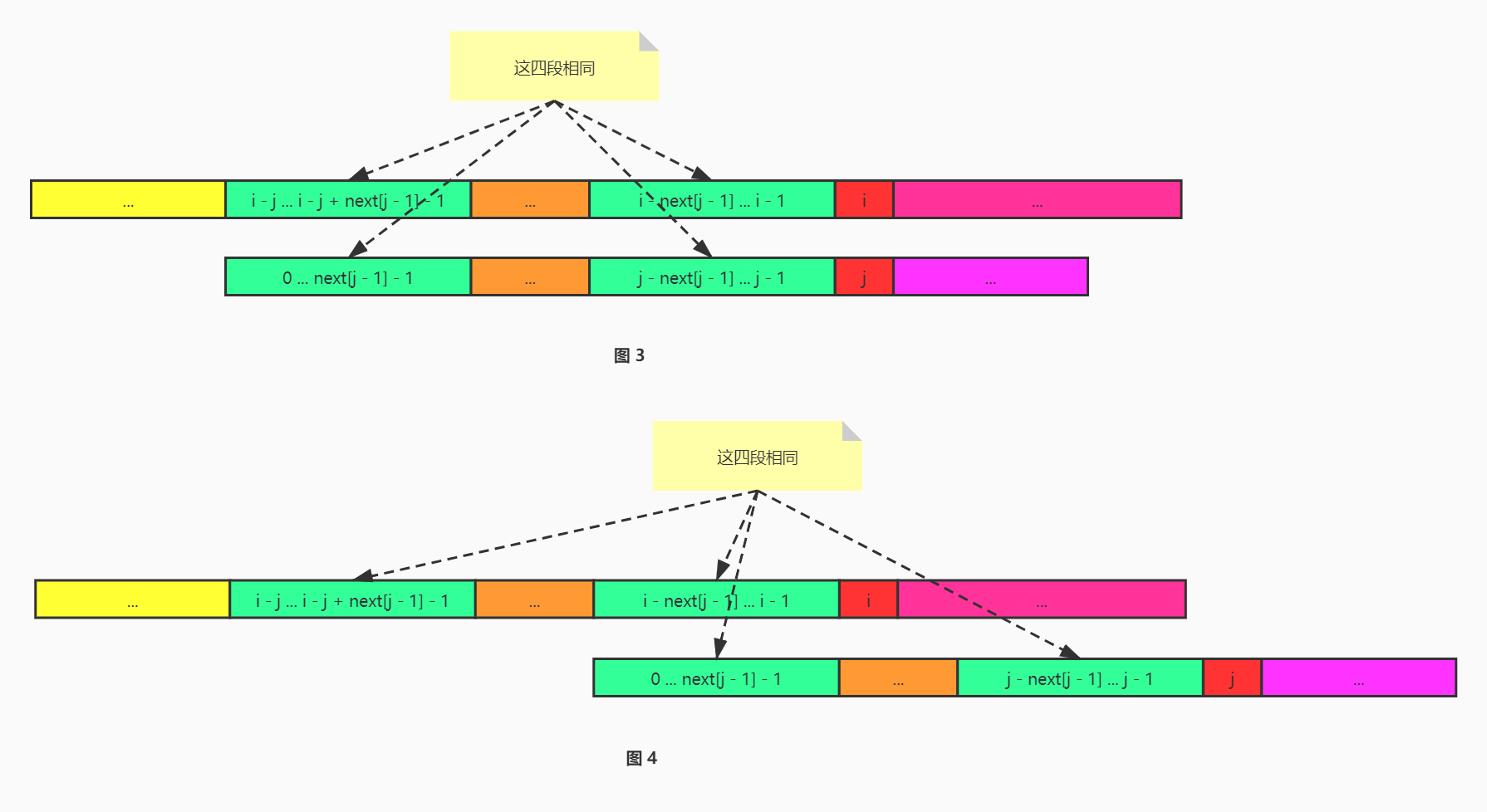
图 3 中 MainString[i - j ... i - 1] 和 Pattern[0 ... j - 1] 匹配，但 MainString[i] 和 Pattern[j] 失配，此时，需要回溯。

在 KMP 算法中，MainString 无需回溯，Pattern 回溯到 next[j - 1]，此即本文开头所讲的跳跃性。

Python 实现

tim-chow 的 Github